Graficando Funciones Cuadráticas

Objetivos de Aprendizaje

·         Graficar ecuaciones cuadráticas en el eje de coordenadas.

·         Definir e identificar las raíces de una ecuación cuadrática.

Introducción

Además de las funciones lineales, uno de los tipos más comunes de funciones polinomiales con las que trabajamos en el álgebra es la función cuadrática. Una función cuadrática es una función que puede ser descrita por una ecuación de la forma y = ax² + bx + c, donde a ≠ 0. Ningún término en la función polinomial tiene un grado mayor que 2. Las funciones cuadráticas son útiles cuando trabajamos con áreas, y frecuentemente aparecen en problemas de movimiento que implican gravedad o aceleración.

Las gráficas de las funciones cuadráticas tienen características que están estrechamente relacionadas con su forma simbólica. A medida que exploremos estas gráficas, aprenderemos a identificar estas características, y veremos algunas de las maneras de estructurar las ecuaciones cuadráticas.

Graficando con Puntos

Una función cuadrática es un polinomio de grado 2, es decir, el exponente más alto en la variable es 2. Los siguientes son ejemplos de funciones cuadráticas:

La función cuadrática más básica y simple tiene la ecuación 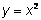. Si hacemos una tabla con los valores de esta función, vemos que el rango (los valores de y, o salida) no se comportan como una función lineal. En una función lineal, el valor de y cambia por la misma cantidad cada vez que el valor de x aumenta por 1. Eso no sucede con una función cuadrática:

x	y = x2
-3	9
-2	4
-1	1
0	0
1	1
2	4
3	9

Los valores de y no cambian por una cantidad constante. Grafiquemos algunos puntos para ver cómo se vería la función:

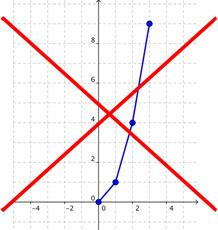
Después de graficar algunos puntos, podría ser tentador conectar los puntos con segmentos de línea, que son rectos. Pero esto estaría mal, y produciría un patrón que no representa la función.

Borremos esas líneas rectas y grafiquemos el resto de los puntos:

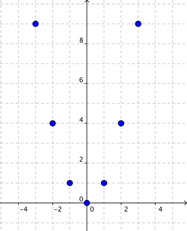
Ahora dibujamos una curva suave conectando los puntos.

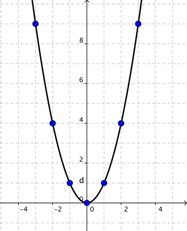
¡Mejor! Una función cuadrática resulta en una gráfica con forma de U, llamada parábola. Los valores de la función cambian suavemente, por lo que la curva debe ser suave también. Ahora que podemos ver la naturaleza de la parábola (forma de U), veamos su forma en detalle.

Características de una Parábola

La forma estándar de una ecuación cuadrática es 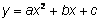. Por ejemplo 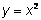, el valor del coeficiente a es 1, y b y c son 0. Si bien muchas ecuaciones cuadráticas presentan valores de b y c diferentes de cero, la gráfica resultante siempre será una parábola.

Las parábolas tienen muchas propiedades que pueden ayudarnos a graficar ecuaciones cuadráticas. Una parábola tiene un punto especial llamado vértice; este es el punto donde la U "da la vuelta". Nota que en el vértice, la parábola cambia de dirección:

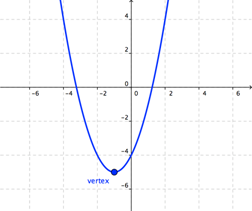
El vértice es el punto más alto o más bajo de la curva, dependiendo si la U se abre hacia arriba o hacia abajo. En el caso de que la parábola abra hacia arriba, el vértice será su punto más bajo; y una parábola que abre hacia abajo, tendrá un vértice en su punto más alto.

Todas las funciones parabólicas tienen un eje de simetría vertical, una línea imaginaria que pasa a través de la mitad de la forma de U y la divide en dos mitades que son imágenes de espejo una de la otra. El eje de simetría siempre pasa por el vértice. Cualquier par de puntos con el mismo valor de y estarán a la misma distancia del eje. En la gráfica interactiva siguiente, haz clic y arrastra el punto A y ve cómo se mueve el punto A'. Nota que el eje de simetría actúa como un espejo entre A y A’.